Любители уникального дизайна плитки на полу или в ванной получили неожиданный подарок от дизайнера Дэвида Смита из британского Йоркшира. Он сумел разгадать математическую загадку, над которой бились без малого 60 лет. Можно ли создать плитку такой формы, чтобы выложенный из нее узор не повторялся ни на одном участке — независимо от размеров площади, которую он покрывает?
Ответ был получен еще в 1960-х – разумеется, можно. Загвоздка в том, сколько плиток разной формы нужно для создания такой апериодической структуры. Первая версия решения содержала 20 000 отдельных видов плитки. Математики взялись за дело и постепенно сократили количество плиток, пока сэр Роджер Пенроуз не сумел достичь (как тогда казалось) идеала. Его «Мозаика Пенроуза» состояла всего из двух видов плиток, из которых можно было выложить какие угодно неповторяющиеся узоры.

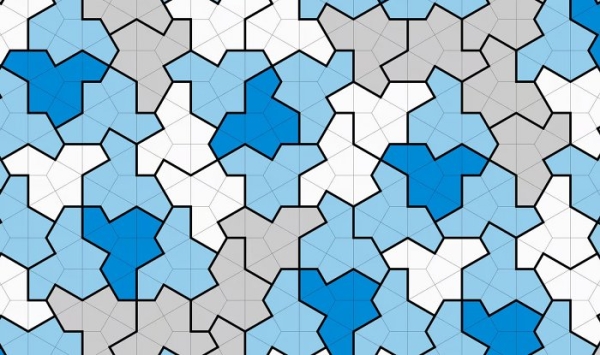
С тех пор ученые пытались понять, возможно ли создать апериодичную плитку всего из одной формы. Дэвид Смит стал первым, кому это удалось, а профессор Крейг Каплан написал программу, которая помогла проверить соблюдение условий апериодичности на площадях произвольного масштаба, включая гигантские. Плитка получила название «Шляпа» (the Hat).
Уже после создания «Шляпы» стало понятно, что с небольшими вариациями формы можно создать немалое количество аналогичных плиток. Однако профессор Каплан уверен, что существуют принципиально иные варианты плиток, которые также соответствуют правилу неповторяемости